Brief Description
Aims and Objectives
Prerequisites
Equipment and Planning
Section A - Simple Simulations
Section B - Random Numbers
Section C - More Simulations
Answers
Test Questions
Test Questions - Answers
Connections with Other Units
|

|
Brief Description
The central theme is that of using simulation to model real-life
situations. Children often collect sets of cards; the first
simulation investigates how long it would take to collect a set
of four. Other simulations use dice and random numbers to model
booking seats on a minibus, finding the right key for a door, the
weather and being stopped at traffic lights.
Design time: 5 hours (B4 and C3
optional)
Aims and Objectives
On completion of this unit pupils should be able to set up,
and improve if necessary, a simulation using (i) playing cards, (ii)
a die, and (iii) a random number table; to model simple real-life
situations.
They will have practised the use of a random number table to
select series of random numbers to suit varying probability
requirements.
They meet examples of everyday situations which can be rephced
(to various degrees of accuracy) by simple probability models and
simulated in the classroom.
They should be more aware of the advantages and possible
disadvantages of replacing real-life situations by models.
Prerequisites
Pupils should be familiar with simple fractions and
proportions, and should be able to mrry out division to one
decimal place.
Equipment and Planning
Dice and packs of playing cards are required for the class,
ideally one for each pair of pupils.
The record pages R1 to R3 contain blank tables and answers to
be completed. Page R4 is a set of random number tables.
Concepts in probability are rather difficult; consequently the
success of this unit depends greatly on the level of
participation of the teacher. It is not recommended that this
material be treated wholly as individually-based learning.
Section A is intended for all pupils and
develops the idea of a simulation as an experiment which models
the essential features of the real-life situation. Two problems
are investigated: the collection of sets of cards, or the like,
and the operation of a minibus service.
Section B introduces random numbers and
random number tables. B4 is optional, designed for more
able pupils, and develops the use of random numbers beyond the
general demands of the unit.
Section C provides further practice in the
use of random numbers by modifying the minibus example. It
introduces two further, more sophisticated situations (one
optional in C3, again for more able pupils): key
selection and the passage through two sets of traffic lights.
Detailed Notes
When probability is used to model real-life situations, the
calculations can become quite complex. This is apparent from the
theoretical solutions presented later.
This unit helps pupils build up an intuition for such ideas.
It shows how real-life events can be likened to random processes
by assigning and combining the relevant probabilities. The rules
of probability are thus being built on intuitive foundations.
Monte Carlo methods are used - this means using random numbers
for simulating chance events. A single trial is unpredictable,
but repeated trials indicate the distribution of results that
might be expected. This requires many results. It is suggested
that class results be combined, though it is essential that all
pupils do some simulations individually. They then develop a
feeling for probability by seeing random events in different
settings.
As described in Section A below, it is better to
start with random number generators: spinning discs, tossing
coins, throwing dice, etc. Class results can be used to
illustrate that all digits, pairs of digits, and so on appear
independently and with equal frequency in the long run.
These features of random numbers are crucial and could be
emphasized by using biased spinners. They are also considered in
the Level One unit Being Fair to Ernie.
The object is to develop a feel for random numbers.
The simulations in this unit use randomizing devices to model
ideal problems.
Teachers desiring to find out more about theoretical aspects
of simulation could consult the following books.
- Monte Carlo Methods, by J. D. Hammersley and D.
C. Handscomb, (Methuen, London, 1964.) This deals with
some of the theory.
- The Teaching of Probability and Statistics, A.
Engel in L. Rade (ed) (Almqvist and Wiksell, Stockholm,
1970; distributed in this country by John Wiley). This
looks at some simulations that can be done by
schoolchildren.
Section A
We suggest that you introduce this section with a class
demonstration and discussion. Throw a die, call Heads if
an even number results, call Tails when odd. Repeat this
several times, then ask the pupils to guess the rule.
Alternatively, call Boy for odd and Girl for
even to simulate births by sex.
This can lead to the consideration of the possible advantages
and disadvantages of simulations: speed, convenience, danger of
over-simplification. One can then show that many aspects of the
real world can be considered as chance events that can be
modelled by the appropriate use of random numbers, for example,
male/female birth, car/van passing, rain/dry.
Thus instead of a real process, it is sufficient to show the
output of a randomizing device, even though equally likely
probabilities may not be involved. This is the essence of Monte
Carlo methods.
Two particular simulations are suggested in the pupil notes
for discussion. Tossing a coin four times can simulate the number
of boys and girls in a family, using Heads for girls
and Tails for boys. Book cricket is a game
played by following a text and using a = maiden ball, b
= bowled, c = caught, d = 2 runs, e =
1 run, f = 4, g = 6, etc.
Pupils may well have their own rules for this game, which is
not a particularly realistic model of a game of cricket, since
little attempt has been made to match up the probabilities.
Pupils may benefit from a demonstration of A1 and A2
from the teacher. If resources are short, A1 and A2
could be attempted by different parts of the class. A whole pack
of cards is not essential, though equal numbers of each suit are;
the replacement of cards is necessary if there are only a few
cards, but this is difficult to organize.
A1
The first example should be familiar to pupils, and the
teacher may find current examples a useful aid.
Questions a, b and c
are intended for discussion and could be extended further if
required to d 6 cards and e 12
cards.
The pupils may require some help in the execution of the
experiment. Teachers may consider the use of a flow chart to
clarify instructions. A blank table, Table 2, on page Rl is
provided for recording the results. Collect the class results for
pupils to use in A2.
A2
The cards involve selection without replacement, and so
the probabilities do change after each card is drawn. This makes
it slightly quicker to collect a set (the mean is reduced by
about 0.3). It should take, on average, about eight cards to
complete a set, but the distribution is rather skewed. c
is rather difficult theoretically.
Class results could be collected with a table running from 4 (the
least necessary) to about 25, though theoretically 40 might be
required. If there is time, a bar chart could be drawn to
illustrate the skewed distribution.
A3
The minibus problem is a standard one with bookings: it
is binomial with n = 12 and p = 1/6.
An owner would probably not overbook, but with present economic
stringencies it might make the difference between profit and loss.
However, overbooking can result in disgruntled customers who are
turned away. Certainly airlines have overbooked and been taken to
court for it.
Here dice are used to simulate chance, and pupils may need
extra guidance on how to perform the experiment and fill the
table. Table 3 on page Rl is provided for recording individual
results. Class results should be collected and discussed, as five
is rather a small sample size.
Question c is a comment on individual
experiments and may be taken up as part of the class discussions
arising from d and e.
It is possible that an unacceptable number of people may be
turned away. The equally likely hypothesis is tenuous. People may
come without booking. Demand may vary.
Section B
Random numbers are introduced in this section. Pupils may
experience difficulties and will certainly benefit from class
discussion, with considerable teacher involvement.
It may be useful to try to show children that numbers called
out by them 'at random' are not really random. Ask them all to
write down a number 'at random' choosing from the numbers 0 to 9.
Collect the results. Usually there are fewer zeros than would be
expected from genuine random numbers.
A point worth stressing is how to get a probability of 1 in 6,
by ignoring 7,8,9 and 0. One could introduce modulo method (as
outlined in B2 for a chance of 1 in 2) but this is left
to the discretion of the teacher.
Brighter pupils may appreciate trying to make more efficient
use of the random number tables by minimizing the number of
digits that have to be discarded. Thus a probability of l in 3 is
the same as 3 in 9, and all digits 1 to 9 can be used with only
the zero being discarded. 4 out of 7 is the same as 56 out of 98,
and so a more efficient use of two-figure random numbers can be
made, and so on.
The use of random numbers is also covered in the Level One
unit Being Fair to Ernie.
B1
If time is available, pupils could usefully construct
and use their own table of random numbers from dice throws.
B2
Page R2 provides copies of the extract of the random
number table used in illustrations and can be used as a work-sheet.
You might like to consider the introduction of the following
method for a chance of 1 in 2:
If the number is 0,2,4,6 or 8, the event takes place.
If the number is 1,3,5,7 or 9, the event does not take place.
B3
This is a further development of the ideas in B2.
The results obtained in B2a, b,
and c, may be helpful in B3a, c
and d.
You might consider using local weather data to relate to local
events. For example how many school cricket matches are likely to
be rained off this season, based on the proportion of days when
there is sufficient rain to cause this. Another possibility is to
consider how many times a week you are likely to have to water an
outside plant which requires water or rain every other day.
The data used to introduce this section was obtained from Sheffield
Weather Summary 1976 (Sheffield City Museums).
The random numbers model is quite crude, since it implies
independence of weather from day to day.
If 3 in 5 is written as 6 in 10, the simulation can use all
the random numbers with:
If the number is 1,2,3,4,5 or 6, it rains.
If the number is 7,8,9 or 0, it does not rain.
*B4
This section is optional and intended for more able
pupils. It applies the ideas already introduced to probabilities
requiring the selection of two-digit random numbers.
You may consider refining methods for b 7 in
30, and d 1 in 13, to make more efficient use of
the random number table.
Section C
In this section we return to the minibus problem and introduce
other situations which can be simulated with the help of the
random number table provided with this unit.
C1
Another piece of information is introduced in the
minibus problem. This is designed mainly to afford pupils
practice in the use of random numbers without making them
consider something new.
Table 4 on page R1 is provided for recording individual
results. Again, it would be helpful to compile class results
before the discussion. In the discussion, you may wish to include:
- Have any important features been ignored?
How might they be taken into account?
C2
This situation may be introduced by demonstrating with,
say, three similar keys for a classroom or cupboard door. The
three ways of choosing should confirm what one could guess
beforehand yet it is still worthwhile to show how one can use the
simulations. The advantage of the simulations is that it gives
some measure of the difference in efficiency between the various
methods. This would take a long time experimentally. If time is
short, only one simulation need be done, but it is desirable to
use several to show how you can adapt the basic model to fit the
different situations.
Tables 5, 6 and 7 on page R3 are provided for the recording of
the results of a, b and c
respectively.
C3
This section is optional and is intended for more able
pupils. Class results could be compiled before answering e.
The traffic light example can be illustrated by a tree diagram:
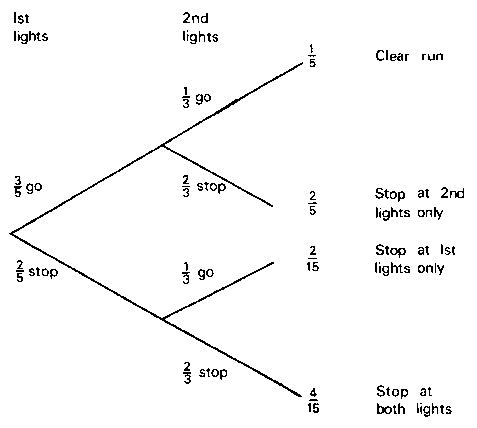
If built-up by pupils or on the blackboard, red and green
lines may enhance this diagram.
The experimental proportions will not be identical to the
theoretical probabilities, but the multiplication rule will still
hold. This can be used with more able pupils to help lay the
foundations of multiplication of probabilities.
Answers
| A1 |
a |
See detailed notes. |
| |
b |
See detailed notes. |
| |
c |
See detailed notes. |
| |
|
|
| A2 |
a |
The mean should be about 8. |
| |
b |
4 and 40 are the minimum and maximum
possible values. |
| |
f |
See detailed notes. |
| |
g |
See detailed notes. |
| |
|
|
| A3 |
b |
Using binomial with n = 12, p
= 1/6 theoretical answers for five
trials are: 1.35, 0.56, 1.48, 1.61. |
| |
c |
See detailed notes. |
| |
d |
See detailed notes. |
| |
e |
See detailed notes. |
| |
|
|
| B1 |
a |
5 1 9 3 7 |
| |
|
|
| B2 |
|
Many possibilities, e.g. |
| |
a |
1 the person does not come
2,3,4,5, the person does come
6,7,8,9,0, ignore |
| |
b |
Use 1; 2,3,4,5,6,7,8; 9,0; as the three
categories. |
| |
c |
Use 1; 2 to 9 and 0; as the first two
categories. |
| |
|
|
| B3 |
|
Many possibilities e.g. |
| |
a |
Use 1,2; 3,4,5; 6,7,8,9,0; as the three
categories. |
| |
b |
Use 1,2,3,4; 5,6,7; 8,9,0; as the three
categories. |
| |
c |
Use 1,2,3; 4,5,6,7,8; 9,0; as the three
categories. |
| |
d |
Use 1,2,3; 4,5,6,7,8,9,0; as the first
two categories. |
| |
|
|
| C1 |
|
Results will vary. |
| |
|
|
| C2 |
a |
The mean should be about 6. |
| |
|
The mean should be about 51/6. |
| |
|
The mean should be about 31/3. |
| |
|
|
| C3 |
a |
3/5. |
| |
b |
1/3. |
| |
f |
The exact probabilities are 4/15,
8/15, 1/5 |
Test Questlons
- By giving an example explain what is a simulation.
- Write down two advantages and one disadvantage of a
simulation.
- In a list of random numbers, what is the chance that the
next number will be:
- 7
- An even number
- The chance that Fred wakes up late is 2 in 7.
We can simulate this using random numbers:
If the number is 1, 2 Fred wakes up late.
If the number if 3,4,5,6,7 Fred does not wake up late.
From the list of random numbers given below:
- Make out a list of the random numbers you would
need for the experiment.
- Underline each number in your list which means
that Fred is late.
5 2 1 4 8 9 5 6 6 5 9 4 1 3 0 8 0 3 1 8
1 0 0 4 2 3 9 4 3 5 6 3 4 2 8 6 6 7 2 6
- Write down a rule for simulating a chance of
- 1 in 8
- 2 in 5
- 4 in 9
- The Sheffield Weather Summary 1976 shows that
there were six rainy days in April 1976. Describe a
simulation to find out how many rainy days there would be
in one week.
Answers
- An experiment which uses a randomizing device to model
another situation.
- Advantages: quick and easy
Disadvantages: may not be a very good model
-
- 1/10
- 1/2
-
- 5 2 1 4 5 6 6 5 4 1 3 3 1
1 4 2 3 4 3 5 6 3 4 2 6 6 2 6
- 5 2 1 4 5 6 6 5 4 1 3 3 1
1 4 2 3 4 3 5 6 3 4 2 6 6 2
6
- e.g.
- 1; 2,3,4,5,6,7,8; 9,0; are the three categories.
- 1,2; 3,4,5; 6,7,8,9,0; are the three categories.
or 1,2,3,4; 5,6,7,8,9,0; are the first two
categories.
- 1,2,3,4; 5,6,7,8,9; 0; are the three categories.
- P(rain) = 6/30 = 1/5
= 2/10
Use 1,2 for a rainy day,
3,4,5,6,7,8,9,0 for a non-rainy day.
Read off seven random digits to find out the simulated
number of rainy days.
Connections with Other Published Units from the Project
Other Units at the Same Level (Level 1)
Shaking a Six Being
Fair to Ernie
Wheels and Meals
Probability games
Practice makes Perfect
Leisure for Pleasure
Tidy Tables
Units at Other Levels In the Same or Allied Areas of the Curriculum
Level 2
On the Ball
Seeing is Believing
Fair Play
Getting it Right
Level 3
Car Careers
Net Catch
Cutting it Fine
Multiplying People
Level 4
Choice or Chance
Testing Testing
This unit is particularly relevant to: Mathematics.
Interconnections between Concepts and Techniques Used In these Units
These are detailed in the following table. The code number in
the left-hand column refers to the items spelled out in more
detail in Chapter 5 of Teaching Statistics 11-16.
An item mentioned under Statistical Prerequisites
needs to be covered before this unit is taught. Units which
introduce this idea or technique are listed alongside.
An item mentioned under Idea or Technique Used is not
specifically introduced or necessarily pointed out as such in the
unit. There may be one or more specific examples of a more
general concept. No previous experience is necessary with these
items before teaching the unit, but more practice can be obtained
before or afterwards by using the other units listed in the two
columns alongside.
An item mentioned under Idea or Technique Introduced
occurs specifically in the unit and, if a technique, there will
be specific detailed instruction for carrying it out. Further
practice and reinforcement can be carried out by using the other
units listed alongside.
| Code No. |
Statistical
Prerequisites |
|
| |
None |
|
| |
Idea or Technique Used |
Introduced in |
Also Used in |
| 1.2a |
Using discrete data |
Seeing is Believing |
Shaking a Six
Wheels and Meals
Leasure for Pleasure
Fair Play
Car Careers
Cutting it Fine
Being Fair to Ernie
Probability Games
Tidy Tables
Getting it Right
Net Catch
Multiplying People |
| 1.3a |
Sampling from small, well-defined,
population |
|
Fair Play
Net Catch |
| 1.3c |
Sampling from distributions or infinite
populations |
Getting it Right |
Fair Play
Net Catch |
| 3.2a |
Dispersion in a distribution or
population |
|
Practice makes Perfect |
| 4.1f |
Using relative frequency to estimate
future probabilities |
On the Ball,
Testing Testing |
|
| 5u |
Inference from bar charts |
Car Careers
Multiplying People |
Probability Games
Practice Makes Perfect |
| 5x |
Comparing actual with expected values |
Being Fair to Ernie
On The Ball
Fair Play
Choice or Chance
Testing Testing |
Probability Games
Car Careers |
| |
Idea or Technique
Introduced |
Also Used
in |
| 1.3e |
Variability in samples |
Being Fair to Ernie
On The Ball
Car Careers
Choice or Chance
Probability Games
Fair Play
Net Catch
Practice Makes Perfect
Getting it Right
Cutting it Fine |
| 1.3f |
Random numbers |
Being Fair To Ernie |
| 1.3g |
Random number tables |
Being Fair To Ernie
On the Ball
Multiplying People |
| 2.1a |
Constructing single variable frequency
tables |
Being Fair to Ernie
Practice Makes Perfect
On The Ball
Choice or Chance
Wheels and Meals
Leasure for Pleasure
Seeing is Believing
Probability Games
Tidy Tables
Car Careers |
| 3.1c |
Mean for small data set |
Practice makes Perfect
Fair Play
Net Catch
On the Ball
Getting it Right
Cutting it Fine
Seeing is Believing
Car Careers |
| 3.2a |
Range |
Practice Makes Perfect
Cutting it Fine |
| 4.1m |
Fairness and equally likel;y
probabilities |
Probability Games
Fair Play
Choice or Chance |
| 4.1n |
Probabilies of a combination of events |
Probability Games
Fair Play |
| 4.3o |
Simulation as a model |
Net Catch |
| 4.3p |
Setting up a simulation |
On the Ball
Testing Testing
Net Catch
Choice or Chance |
| 4.3q |
Interpreting a simulation |
On the Ball
Net Catch
Choice or Chance
Testing Testing |
| 5a |
Reading tables |
Shaking a Six
Probability Games
On the Ball
Net Catch
Being Fair to Ernie
Leasure for Pleasure
Seeing is Believing
Multiplying People
Wheels and Meals
Tidy Tables
Car Careers
Testing Testing |
Page R1
| Trial |
Guess |
Number of cards used |
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
Totals
|
|
|
Table 2
| Trip |
Person |
Total
number
of seats filled |
Tick if
minibus is
over-booked |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 3
| Trip |
Person |
Total
number
of seats filled |
Tick if
minibus is
over-booked |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 4
Page R2
| a |
For a
probability of 1 in 5:
| If the number is |
|
the person does
not come. |
| If the number is |
|
the person does
come. |
| If the number is |
|
we go to the
next number. |
| 9 |
1 |
9 |
3 |
8 |
8 |
5 |
6 |
3 |
5 |
| 7 |
6 |
9 |
7 |
3 |
5 |
1 |
9 |
3 |
7 |
| 1 |
4 |
6 |
6 |
0 |
7 |
4 |
6 |
5 |
0 |
| 5 |
8 |
0 |
8 |
7 |
3 |
4 |
2 |
9 |
7 |
| 2 |
0 |
4 |
2 |
6 |
4 |
6 |
8 |
0 |
0 |
So a
list we could use is
|
| b |
For a
probability of 1 in 8:
| If the number is |
|
the person does
not come. |
| If the number is |
|
the person does
come. |
| If the number is |
|
we go to the
next number. |
| 9 |
1 |
9 |
3 |
8 |
8 |
5 |
6 |
3 |
5 |
| 7 |
6 |
9 |
7 |
3 |
5 |
1 |
9 |
3 |
7 |
| 1 |
4 |
6 |
6 |
0 |
7 |
4 |
6 |
5 |
0 |
| 5 |
8 |
0 |
8 |
7 |
3 |
4 |
2 |
9 |
7 |
| 2 |
0 |
4 |
2 |
6 |
4 |
6 |
8 |
0 |
0 |
So a
list we could use is
|
| c |
For a
probability of 1 in 10:
| If the number is |
|
the person does
not come. |
| If the number is |
|
the person does
come. |
| If the number is |
|
we go to the
next number. |
| 9 |
1 |
9 |
3 |
8 |
8 |
5 |
6 |
3 |
5 |
| 7 |
6 |
9 |
7 |
3 |
5 |
1 |
9 |
3 |
7 |
| 1 |
4 |
6 |
6 |
0 |
7 |
4 |
6 |
5 |
0 |
| 5 |
8 |
0 |
8 |
7 |
3 |
4 |
2 |
9 |
7 |
| 2 |
0 |
4 |
2 |
6 |
4 |
6 |
8 |
0 |
0 |
So a
list we could use is
|
Page R3
| Trial |
Key |
Number of
keys tried |
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
Table 5
| Trial |
Key |
Number of
keys tried |
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
Table 6
| Trial |
Key |
Number of
keys tried |
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
Table 7
| Trial |
Stopped at
first lights |
Stopped at
second lights |
Number of
times stopped |
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
| 5 |
|
|
|
| |
|
|
|
| 6 |
|
|
|
| 7 |
|
|
|
| 8 |
|
|
|
| 9 |
|
|
|
| 10 |
|
|
|
| |
|
|
|
| 11 |
|
|
|
| 12 |
|
|
|
| 13 |
|
|
|
| 14 |
|
|
|
| 15 |
|
|
|
| |
|
|
|
| 16 |
|
|
|
| 17 |
|
|
|
| 18 |
|
|
|
| 19 |
|
|
|
| 20 |
|
|
|
Table 8
Page R4
Random Numbers
| 77 04 01 09 73 89 84 35 77 76 12 39 43 64 97 40 83 99 18 26 |
| 39 00 29 43 44 23 01 92 63 88 89 61 91 67 90 04 22 34 19 93 |
| 63 78 56 92 64 87 82 73 33 53 25 36 40 91 19 52 36 40 91 19 |
| 52 67 36 19 67 84 34 55 97 37 92 30 27 26 71 04 71 78 38 15 |
| 58 21 59 06 07 57 57 99 40 43 47 18 03 62 91 41 60 90 45 13 |
| |
| 24 65 06 55 72 04 87 31 29 39 56 29 93 95 65 90 95 99 87 46 |
| 66 36 07 93 49 20 02 59 48 54 35 73 34 68 72 44 28 87 44 81 |
| 09 77 10 52 52 52 65 29 15 82 81 23 56 99 82 21 01 62 81 98 |
| 14 56 32 69 71 27 29 74 87 24 79 42 66 10 50 75 47 87 08 26 |
| 35 84 64 56 47 54 11 22 93 84 75 65 06 91 47 47 67 25 97 25 |
| |
| 08 35 58 94 06 04 02 41 56 90 12 38 09 87 20 22 20 30 72 51 |
| 39 84 92 69 36 47 42 09 72 28 20 63 90 67 24 56 54 27 12 89 |
| 16 20 61 32 75 91 50 16 53 51 83 14 30 93 83 74 59 31 70 81 |
| 54 35 42 49 55 57 13 50 70 03 72 39 48 67 94 73 37 67 13 39 |
| 66 29 74 71 55 60 88 08 10 62 08 10 55 28 51 86 52 75 00 14 |
| |
| 59 00 51 60 44 72 59 53 94 22 10 74 38 54 43 43 45 29 91 74 |
| 43 45 29 91 74 43 58 08 72 99 89 09 38 66 75 45 49 00 47 42 |
| 75 47 88 59 25 21 04 61 07 14 40 73 42 68 67 25 68 76 98 45 |
| 28 80 46 57 74 80 62 57 51 32 33 42 06 56 17 81 94 25 05 63 |
| 58 62 21 99 86 58 90 78 87 05 96 57 38 14 37 35 05 51 87 25 |
| |
| 87 71 56 03 65 03 11 69 23 98 78 64 52 19 04 99 04 73 90 48 |
| 41 21 95 96 34 83 03 16 31 72 11 50 65 47 58 80 68 92 79 82 |
| 77 93 27 40 49 08 05 83 42 49 80 95 99 46 24 51 85 74 13 83 |
| 81 27 96 24 42 13 33 55 25 65 91 39 43 36 83 32 40 32 48 71 |
| 93 44 83 25 03 62 06 48 98 74 38 18 76 63 58 44 87 58 91 26 |
| |
| 47 04 95 29 28 67 85 59 17 41 49 89 23 35 50 90 28 97 55 86 |
| 20 52 82 47 00 24 00 46 69 91 07 37 21 93 54 92 73 09 06 08 |
| 36 67 47 47 03 16 69 50 48 41 70 97 26 43 30 52 10 16 85 03 |
| 35 60 74 94 29 84 89 72 57 65 49 30 11 61 54 88 18 85 68 32 |
| 37 80 42 50 20 09 57 58 41 58 42 62 17 11 94 98 81 98 04 49 |
| |
| 10 91 74 06 38 02 57 04 25 67 52 47 72 59 62 22 42 44 98 26 |
| 10 17 59 75 76 74 67 12 19 68 34 28 32 54 11 80 14 51 42 07 |
| 42 45 57 52 07 84 44 43 01 65 20 56 64 01 46 39 26 73 83 92 |
| 01 61 18 96 23 36 41 01 57 70 20 29 64 90 49 77 41 32 85 93 |
| 74 91 20 66 07 62 81 51 40 58 26 21 96 98 14 57 69 96 99 86 |
| |
| 30 25 71 25 27 20 69 11 38 51 41 67 45 95 22 35 55 75 36 20 |
| 84 64 38 27 68 61 01 90 31 58 18 77 70 79 15 29 55 10 20 18 |
| 28 69 32 14 56 22 86 70 48 24 83 87 16 63 66 62 21 74 98 04 |
| 38 40 21 06 72 81 04 57 41 98 12 60 98 24 11 51 34 27 02 49 |
| 06 36 38 42 84 53 41 95 37 29 48 68 72 86 22 22 71 76 85 09 |
| |
| 30 36 31 16 12 35 75 25 20 31 83 50 84 83 34 07 37 45 09 73 |
| 18 87 76 43 56 63 19 65 36 86 14 47 86 86 30 97 48 08 80 49 |
| 32 70 17 68 75 98 52 05 67 68 22 94 80 18 05 90 28 45 40 52 |
| 66 60 69 56 87 43 72 87 76 43 40 66 08 77 50 43 70 91 86 54 |
| 32 60 71 47 28 06 21 63 63 16 25 32 21 35 62 47 20 42 08 87 |
| |
| 43 89 32 54 85 23 87 60 87 38 11 47 76 85 83 97 89 52 11 56 |
| 49 55 09 63 51 15 26 48 22 99 40 82 75 31 19 71 87 57 58 67 |
| 00 04 13 23 93 86 64 21 15 55 69 21 19 54 22 57 61 46 85 70 |
| 99 50 06 22 15 92 33 21 68 45 25 97 27 21 06 67 93 15 96 29 |
| 80 62 34 15 07 51 34 99 93 37 31 96 54 85 39 37 94 10 91 51 |
|