Probability Games

Probability Games	Statistics In Your World

Student Notes

Teachers Notes

Odds & Evens

The Results

Unbiased Dice

Which One Happened?

Likely or Unlikely

Assigning Probabilities

Other Dice & Spinners

Adding Two Dice

Multiplying Two Dice

In this unit you will be playing games with dice and coins and looking at the results.

Is it Fair?

Odds & Evens
You will need a die and page RI.
Alan and Brian are playing a game. Each player starts with nine counters. Alan chooses odds, Brian evens.
They throw a die.
For the odd numbers
or or
Alan gains 1 or 3 or 5 counters from Brian.
For the even numbers
or or
Brian gains 2 or 4 or 6 counters from Alan.
They go on playing until one of them runs out of counters.

a	In how many ways can Alan gain some counters?
b	In how many ways can Brian gain some counters?
c	Do you think this is a fair game?

The die shows	1	1	1	4	2	5	5	6	5	4	5	2	3	2	3
Counters gained by	A	A	A	B	B	A	A	B	A	B	A	B	A	B	A

Table 1 - Odds and Evens - Alan and Brian's game

This game took 15 throws altogether.
The first line shows the score on the die. The second line shows who gained counters on that throw.

d	Follow through these results and show that Alan was the winner.

Play the game with a partner. Decide who should be odds and who should be evens.

e	Play the game five times. Record the results of each game on page Rl.
f	How many games did odds win?
g	How many games did evens win?
h	Do you now think the game is fair? Give a reason.

In our game, Alan won some counters nine times, Brian won counters six times.
Look at the results of your games on page R1.

i	From the second line of all five games, find out how many times you each won some counters.
j	Did you each win some counters about the same number of times? Even so, why could the game be unfair?
k	How can you make the game fair?

The Results
You will need:
Pages R1 and R2 and some squared paper.
Alan and Brian looked again at the results of their five games. They made a tally of the number of times each face of the die showed. Their results are given in the following Table 2.

Face	Tally	Number of times
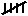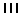		8
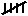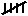		11
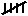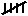		11
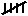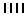		9
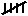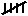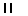		12
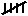		8

Table 2 - Throwing a die: Alan and Brian's results

a	Complete Table 6 on page R2, using the results of your five games.
b	Draw a bar chart (like Figure 1) to show your results.

Remember to label the axes and the chart. You can colour it if you like.

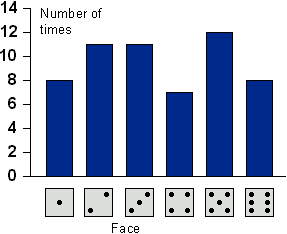
Figure 1 - Throwing a die: Alan and Brian's results

Look at the heights of the bars in your bar chart.

c	Are the bars all nearly the same height?
d	What would you think about the die if one bar was much higher than the others?
e	Do the heights of the bars on your chart vary more than you would expect from a normal die?

Unbiased Dice
If one face of a die turns up considerably more than any other, we say that the die is BIASED.
A die which is not biased is fair, or UNBIASED.
An ordinary die is usually accepted as fair. At any throw, each face has an equal chance of appearing on top. We are as likely to get as or as any other face.
With an unbiased die on a large number of throws, we would expect each face to appear about the same number of times. (Look at your bar chart).
The six faces are equally likely. We say that the probability of getting is ¹/₆ because it is one of six equally likely faces.

a	Copy the following sentence. When throwing a fair die, the probability () = ¹/₆
b	Write down a similar statement for two of the other five faces.

Which One Happened?
An unbiased die was thrown 60 times. The results were recorded in a FREQUENCY TABLE. A frequency table shows how often (frequently) a particular value occurs.
The results are in one of the four columns of Table 3.
The other three have been made up. Look at each one carefully.

Score	Frequency
Score	(i)	(ii)	(iii)	(iv)
	10	12	11	6
	10	14	23	4
	10	8	7	5
	10	11	8	14
	10	9	1	16
	10	6	10	15

Table 3 - Sixty throws of a die.

a	Copy out Table 3.
b	Which results do you think really happened?
c	Why do you think the others were the made-up results? (Drawing bar charts for each column may help you to decide.)

Likely or Unlikely?
It is possible to get each of the results (i), (ii), (iii), (iv) in Table 3 by throwing a die 60 times.
We cannot predict exactly what will happen. We can only say that some results are more likely than others,
or that they are more or less probable than others.

Here is a list of phrases used to describe probabilities

	Very likely, fifty-fifty, probable, impossible, highly improbable, certain, unlikely
a	Try to put them in order, from lowest to highest probabilities. The list is begun below:
	Impossible, __________, __________, fifty-fifty, __________, very likely,__________
	Write down some other words you use to describe probabilities
c	Read through the statements below: It will snow next Christmas Day. You will watch television tonight. You will get to school on time tomorrow (or Monday). You will pass a horse and cart on the way home from school. You will buy a new record next month. You will grow to be taller than your mother. Copy down each statement. Against it write a word from the above list to describe how likely it is to be true.
d	Make up some statements of your own and decide how likely they are.

Assigning Probabilities
Suppose we throw a die.

a	How can we find the probability of getting or

These are two faces out of six equally likely faces.
So probability (getting or ) = ²/₆ = ¹/₃.

Use a similar method to work out the probability of getting:
b	A two or a four
c	Three or less
d	More than four
e	Less than six
f	An even number
g	A multiple of three
h	A seven
i	Six or less
j	Are all of your answers, from a to f, fractions?
k	What words would you use to describe h and i?

If something is impossible, it has probability 0. If something is certain, it has probability 1. All the other probabilities are between 0 and 1. We can also use decimal numbers between 0 and 1 for probabilities.

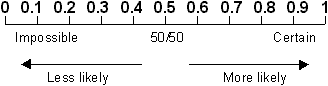
Figure 2 - The probability scale

1	What decimal numbers would you use to describe the probabilities of each of the statements 1 to 6 in A5c?

Other Dice & Spinners
You will need other shaped dice and spinners.

a	Do some experiments to find the probabilities of different faces or sectors.

Adding Two Dice
You will need:
Two dice, nine counters and page R2.
This is a game for two players. Alan and Brian play the game. They throw two dice and add the score shown on each die.
If the sum is 2, 3, 4, 5, 10, 1 1, or 12, Alan takes one counter from the pile. If the sum is 6, 7, 8, or 9, Brian
takes one counter from the pile.
The first player with five counters is the winner. The results of their game are shown in Table 4.

Sum of scores	8	6	7	10	5	7	5	7
Counter won by	B	B	B	A	A	B	A	B

Table 4 - Alan and Brian: Results of adding two dice game

Check that Brian is the winner.

a	Do you think it is a fair game? Give reasons for your answer.
b	Play the game 10 times. One of you is A(for Alan), the other B. Record the results of each game in the same way as the example.
c	How many games did A win?
d	How many games did B win?
e	Make a tally of the results of your 10 games in Table 7 on page R2. Give your results to your teacher.
f	Combine your results with the others from your class. Complete Table 7.
g	Which sum happened most often? Which sum happened least often? (There may be more than one answer to each question.)
h	Do you now think the game is fair? Give a reason.
*i	Design a fair game for adding two dice.

Multiplying Two Dice
You will need two dice and nine counters.
This is a variation of the last game. Throw two dice, and multiply the scores shown on each die.
For a score of less than 13, A takes one counter from the pile. For a score of more than 18, B takes one counter from the pile.
The first player to have five counters wins the game.

a	Who do you think is more likely to win the game?
b	Play the game a few times and try to decide whether it is fair.

Back