Three Coins
One Coin
One Die
Two Coins
Choosing Numbers
Names in a Bag
Fair Game
|

|

Games For Three - Are They Fair?
Here are some games for you to play with two friends. Your
teacher will tell you which to do. For each game you need one
sheet of squared paper each and a pool of 20 counters. The winner
of each game is the one with the most counters at the end. Ann,
Brian and Charles played the games. Use the same rules when you
play.
You will have to decide whether or not each game you play is
fair.
What is a fair game?
When you play each game, start with 20 counters in the middle.
Remember you are trying to find if the games are fair. You are
not finding who can win the most.
Three Coins
You will need three coins, one each.
Ann, Brian and Charles toss their coins. When they are
all Heads or all Tails, they toss again.
When one is different, the off one wins. The winner takes a counter.
Play this game. Repeat until all the counters have been won.
|
a |
Record your results in a table like Table 1. |
| * |
b |
Plot your results on a bar chart like Figure 1. |
|
c |
Do you think the game is fair? Why? |
|
Name
|
Number of counters
|
| Ann |
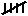 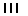 |
8 |
|
| Brian |
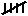  |
6 |
|
| Charles |
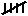  |
6 |
|
Table 1 - Ann, Brian and Charles - three coins
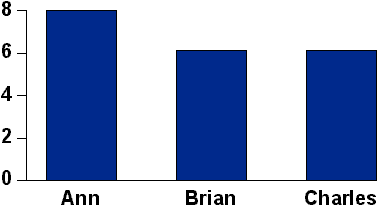
Figure 1 - Three coins - Ann, Brian and Charles's results
One Coin
You will need one coin and squared paper.
Ann tosses the coin and Brian calls. The winner tosses
again and Charles calls. The winner of this toss takes a counter.
Play this game, and repeat until all the counters have been won.
REMEMBER: Always make sure the same two people start.
|
a |
Record your results in a table like Table 1. |
| * |
b |
Plot your results on a bar chart like Figure 1. |
|
c |
Do you think the game is fair? Why? |
One Die
You will need a die.
Ann chooses the numbers 1 and 2, Brian chooses 3 and 4. This leaves 5 and 6 for Charles.
The die is thrown, and the person whose number shows takes a counter.
Each of you choose two numbers like this.
Play the game and repeat until all the counters have been won.
|
a |
Record your results in a table like Table 1. |
| * |
b |
Plot your results on a bar chart like Figure 1. |
|
c |
Do you think the game is fair? Why? |
Two Coins
You will need two coins.
Two coins can fall as two Heads, Head and a Tail or two Tails.
Ann chooses two Heads, Brian chooses Heads and a Tail and Charles has two Tails.
The two coins are tossed, and the winner takes a counter.
Play this game, and repeat until all the counters have been won.
|
a |
Record your results in a table like Table 1. |
| * |
b |
Plot your results on a bar chart like Figure 1. |
|
c |
Do you think the game is fair? Why? |

Choosing Numbers
From the numbers 1,2,3,4,5,6,7,8,9, Ann chooses 1,4,7 and Brian chooses 2,6,9.
This leaves 3,5,8 for Charles but he does not know.
Charles then writes down 20 numbers from 1,2,3,4,5,6,7,8,9.
Ann and Brian then tell Charles his numbers.
Ann takes a counter for each time 1,4 or 7 appears on the list.
Brian does the same for 2,6 or 9, and Charles for 3,5,8.
Play this game choosing your own numbers.
REMEMBER: The one who writes down the numbers does not know who has which numbers.
All the numbers 1,2,3,4,5,6,7,8,9 are shared between three pupils.
|
a |
Record your results in a table like Table 1. |
| * |
b |
Plot your results on a bar chart like Figure 1. |
|
c |
Do you think the game is fair? Why? |
|
d |
If it is not fair how do you think it could be made more fair? |
Names in a Bag
You will need three small equal size pieces of paper and a bag.
Each write your name on one piece of the pieces of paper, fold it in half and put it in the bag.
Mix the pieces of paper up.
Pick out one piece of paper, and read the name.
That person then takes a counter.
Fold the piece of paper again and put it back in the bag.
Repeat until all the counters are won.
|
a |
Record your results in a table like Table 1. |
| * |
b |
Plot your results on a bar chart like Figure 1. |
|
c |
Do you think the game is fair? Why? |
Fair Game
If everyone has an equal chance of winning it is a fair game.
We say they are EQUALLY LIKELY to win.
Look at the games you played.
|
a |
In which games was everyone likely to win? |
|
b |
In these fair games, did everyone win the same number of counters? Why not? |
|
c |
How could you make sure whether or not a game is fair? |
|
d |
Invent an easy fair game to play when there are tow people, and when there are six people. |
|